Ultraproducts of fields, II

Ultraproducts of fields, II June 28, 2008

Posted by Alexandre Borovik in Uncategorized.
trackback

I continue my post on ultraproducts. So, we want to understand in what sense an ultraproduct of finite fields $F_i$ of unbounded order is a limit at infinity of finite fields. The answer now should be obvious: since ultraproducts are residue fields for maximal ideals in the cartesian product

$R = \prod F_i,$

the topology in question should be the canonical topology (Zariski topology) of the spectrum of the ring $\mbox{Spec}(R)$ . It instantly follows from the description of ideals and maximal ideals in $R$ that this is the Stone topology on the set of ultrafilters on $\mathbb{N}$ , or, what is th same, the Cech-Stone compactification $\beta\mathbb{N}$ of the set $\mathbb{N}$ with descrete topology. Therefore the answer is: an ultraproduct is the limit in the Cech-Stone compactification of a discrete countable set.

I have to admit that at this point I reached limits of my knowledge of set-theoretic topology and had to dip into Wikipedia. It happened that $\beta\mathbb{N}$ , and even more so its non-principal part ${\mathbb{N}}^* = \beta{\mathbb{N}} \setminus {\mathbb{N}}$ is characterised by some unique properties: If the continuum hypothesis holds then ${\mathbb{N}}^*$ is the unique Parovicenko space, up to isomorphism.

According to Wikipedia, a Parovicenko space is a topological space X satisfying the following conditions:

X is compact Hausdorff
X has no isolated points
X has weight c, the cardinality of the continuum (this is the smallest cardinality of a base for the topology).
Every two disjoint open F_σ subsets of X have disjoint closures
Every nonempty G_δ of X has non-empty interior.

As you can see, ${\mathbb{N}}^*$ is uniquely characterised by very natural properties.

It is yet another manifestation of of one of the most pardoxical properties of mathematical infinity: canonicity of workable constructions in the infinite domain.

Comments»

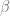1. dcorfield - July 4, 2008: I wonder how much of what is natural about $\mathbb{N}^*$ can be put in category theoretic terms. The $\beta$ you mention is a functor, Stone-Cech compactification, from Top (the category of topological spaces) to CHaus (the category of compact Hausdorff spaces). It is left adjoint to the underlying functor going the other way.

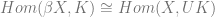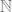So, $Hom(\beta X, K) \cong Hom(X, U K)$ . In the case of $\beta \mathbb{N}$ a map to a compact Hausdorff space is determined by a map from $\mathbb{N}$ to that space.

But does the formation of $\mathbb{N}^*$ by removing the principal part, correspond to a category theoretic construction?

Reply